Translations and coordinate transformation
Julia in Practice: Building Scattering.jl from Scratch (3)
In this post we will implement a submodule translation.jl to perform transformation of a vector in the reference coordinate to the internal coordinate of a scatterer. Translation and coordinate transformation will be discussed in detail.
Table of Contents
Translation and Coordinate Transformation
The core functionality of Scattering.jl is to compute the form factor of an arbitrary scatter. It is convenient to model any scatter as a type which contains all the physical parameters necessary for the form factor computation. The most essential quantities are the position, shape (characteristic lengths for an object with known shape), and the orientation of the object if it is anisotropic. The shape depend on specific object we are actually looking at. Positions and orientations, however, are independent of the type of a scatterer. Therefore, it is possible to develop a general description for them.
A general way to describe the position of an object in space is using the position vector. And the orientation of an object can be conveniently described by a rotation operator. This blog post is devoted to the description of position. And the description of orientation will be deferred to the next post.
The description of positions and orientations strongly depends on which coordinate system they are in. Since all analytical expressions of form factors are assumed in the Cartesian coordinate, hereafter positions and orientations of scatterers are assumed to be expressed in the Cartesian coordinate system.
The most concise references to consult for these subjects are ref12.
Points and Vectors
Although points and vectors can be both expressed in an array of numbers, called components, it is important to note the distinction between them. Points of a Euclidean space form a so-called affine space, and are themselves not vectors, because the “sum” of two points and the “multiplication” of a point by a scalar are not defined. Rather, an affine space has an auxiliary vector space “attached” to it, over which these operations are defined; “differences” between points are uniquely associated with vectors in this auxiliary space:
\[\begin{equation} \vv = p_2 - p_1 \end{equation}\label{eq:vector}\]Once an origin point $o$ and a basis for the vector space are chosen, the coordinates of a point $p$ are the components of the difference vector $p − o$. This special difference vector is known as the position vector. If we let the origin of a Cartesian coordinate coincide with point $o$, then we can express $o$ as a column vector $[0\;0\;0]^T$ (here superscript $T$ denotes matrix transpose). $p$ then is $[p_x\;p_y\;p_z]^T$ expressed in the Cartesian coordinate. And the vector $\vv$ is expressed as $[p_x-0\;p_y-0\;p_z-0]^T = [p_x\;p_y\;p_z]^T$ as well. We say $p_x,\;p_y,\;p_z$ are components of the point $p$ or the vector $\vv$. Thus in this setup, $\vv$ and $p$ have an identical expression in the form of array of components.
One of the most important properties of a vector is that it is invariant under coordinate transformation which means its components are independent of which coordinate system they are in, while the components of a point are just labels in its associated coordinate system and they will change accordingly under coordinate transformation.
Alibi and alias translations
In this project, we are interested in isometric transformations which means distances and angles (thus the shape of an object to be transformed) is preserved after the transformation. For such isometric transformation, however, there are two possible (equivalent) interpretations: alibi (active) and alias (passive). An alibi transformation moves (or rotates) an object to another location while the underlying coordinate system is unchanged.
Figure 1 shows a typical alibi translation. The object at point $p$ with a position vector $\vr$ has been translated to point $p’$ with a position vector $\vr’$. The translation vector is thus
\[\begin{equation} \vt = p' - p \end{equation}\label{eq:alibi_translation_vector}\]And the new position vector of the translated object is
\[\begin{equation} \vr' = \vr + \vt \end{equation}\label{eq:alibi_translation}\]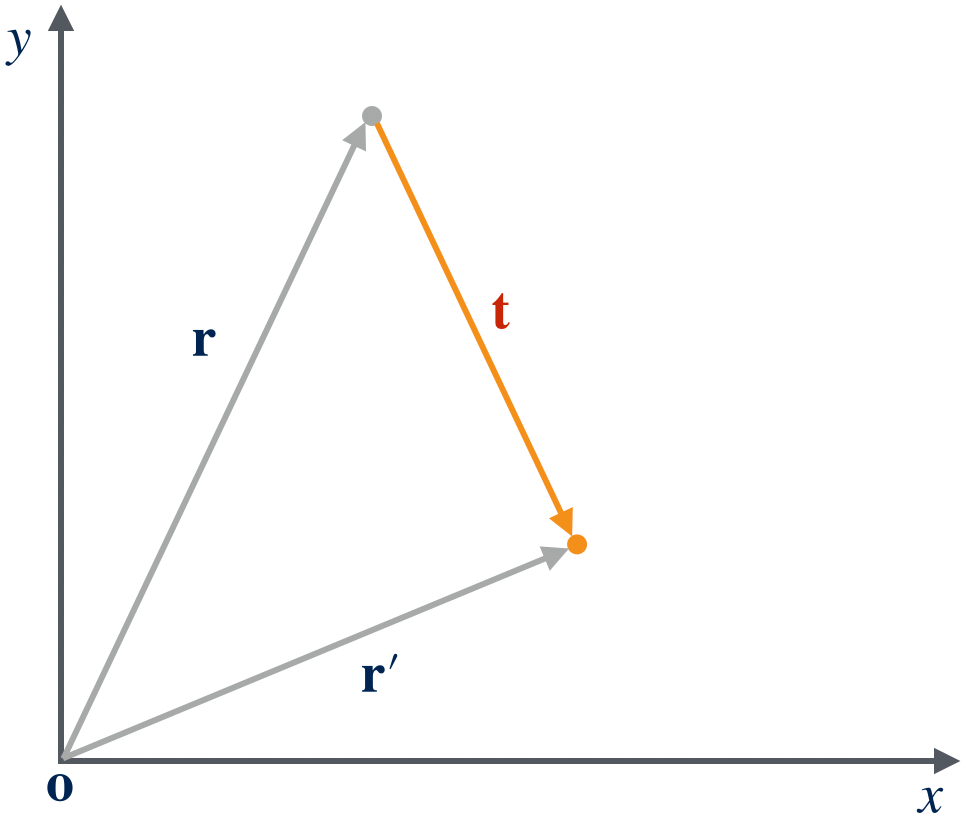
Figure 2 shows a typical alias translation. The old coordinate with its origin at point $o$ (position vector $\vo=[0\;0\;0]^T$) is translated to the new coordinate with its origin at point $o’$ (position vector $\vo’$). It is important to note that the components of $\vo’$ should be expressed in the old coordinate in the following calculations.
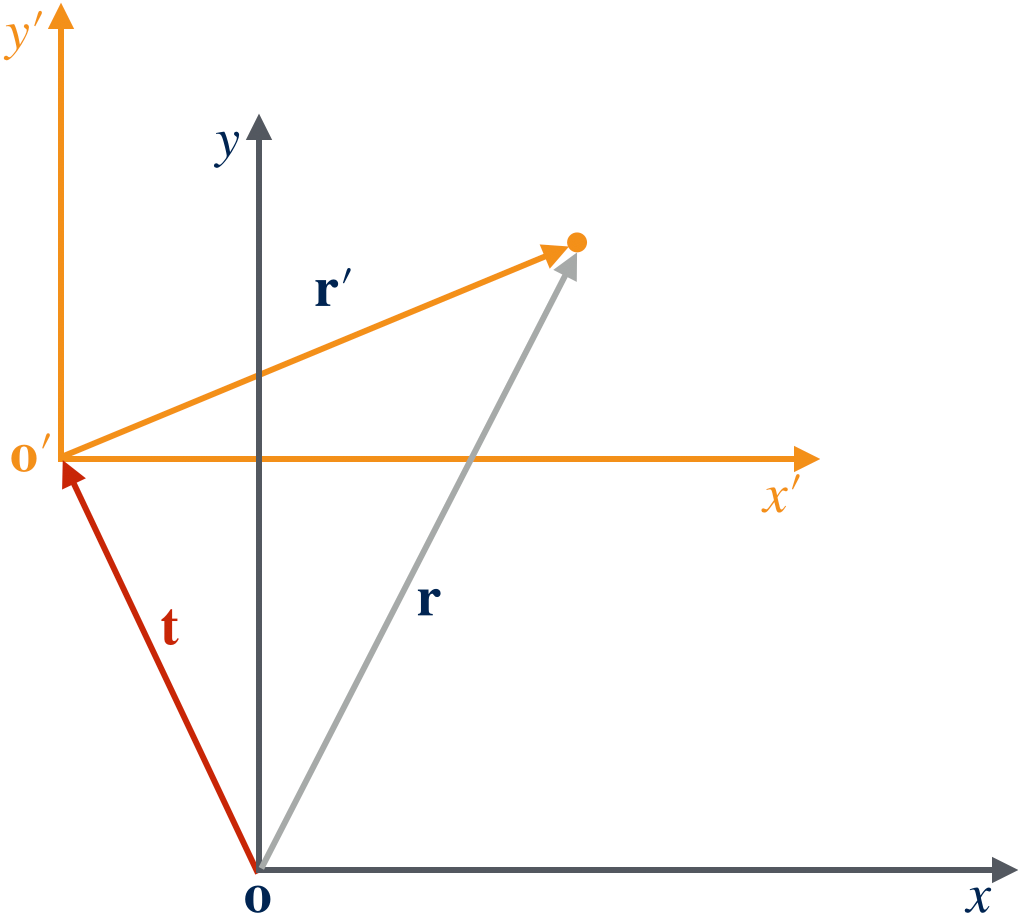
The position of the object in the old coordinate is at point $p$, and it is at point $p’$ in the new coordinate. Note the components of $p$ and $p’$ are different in general. The object’s position vector in the old coordinates is
\[\begin{equation} \vr = p - o \end{equation}\]and in the new coordinate is
\[\begin{equation} \begin{split} \vr' &= p - o' \\ &= p' - \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ &= p'. \end{split} \end{equation}\]The first line is computed in the old coordinate and the second and third line is computed in the new coordinate, where have invoked the property of a vector that it is invariant under coordinate transformation. We can rewrite $\vr’$ as
\[\begin{equation} \begin{split} \vr' &= p - o' \\ &= p - o + o - o' \\ &= \vr - (o' - o). \end{split} \end{equation}\]In the third line, we can then define a translation vector, $\vt$, for the coordinate transformation, which translates the old coordinate to the new coordinate:
\[\begin{equation} \vt = o' - o = \vo'. \end{equation}\label{eq:alias_translation_vector}\]In the aid of the translation vector, we can now compute $\vr’$ as
\[\begin{equation} \vr' = \vr - \vt \end{equation}\label{eq:alias_translation}\]The above formula, however, can be directly read off from Figure 2 using the geometric vector addition rule. Note that in the alias interpretation, the translation vector has an opposite direction to that of the alibi interpretation by comparing \eqref{eq:alibi_translation} and \eqref{eq:alias_translation}.
In the sense of coordinate transformation, we can define a translation operator, $T$, which transform a position vector $\vr$ in the old coordinate to a position vector $\vr’$ in the new coordinate:
\[\begin{equation} \vr' = T\vr = \vr - \vt \end{equation}\label{eq:translation_operator}\]Application of a translation operator on a vector has the meaning that it transforms such vector from the old coordinate to the new coordinate.
Convention we used
In description of the position and orientation of a scatterer, we will adhere to the convention of alias or (passive) transformations. First we shall choose a reference Cartesian coordinate system with its origin at $o=[0\;0\;0]^T$. Then a scatterer with its origin locates at point $o’$ in the reference coordinate. The origin of a scatterer can be chosen as its center of mass or any other particular point that is characteristic to the scatterer. We will create a new Cartesian coordinate with its origin at $o’$. The resulted coordinate is called the internal coordinate system of this particular scatterer. The whole setup is illustrated in Figure 3. The scatterer in Figure 3 is an ellipse.
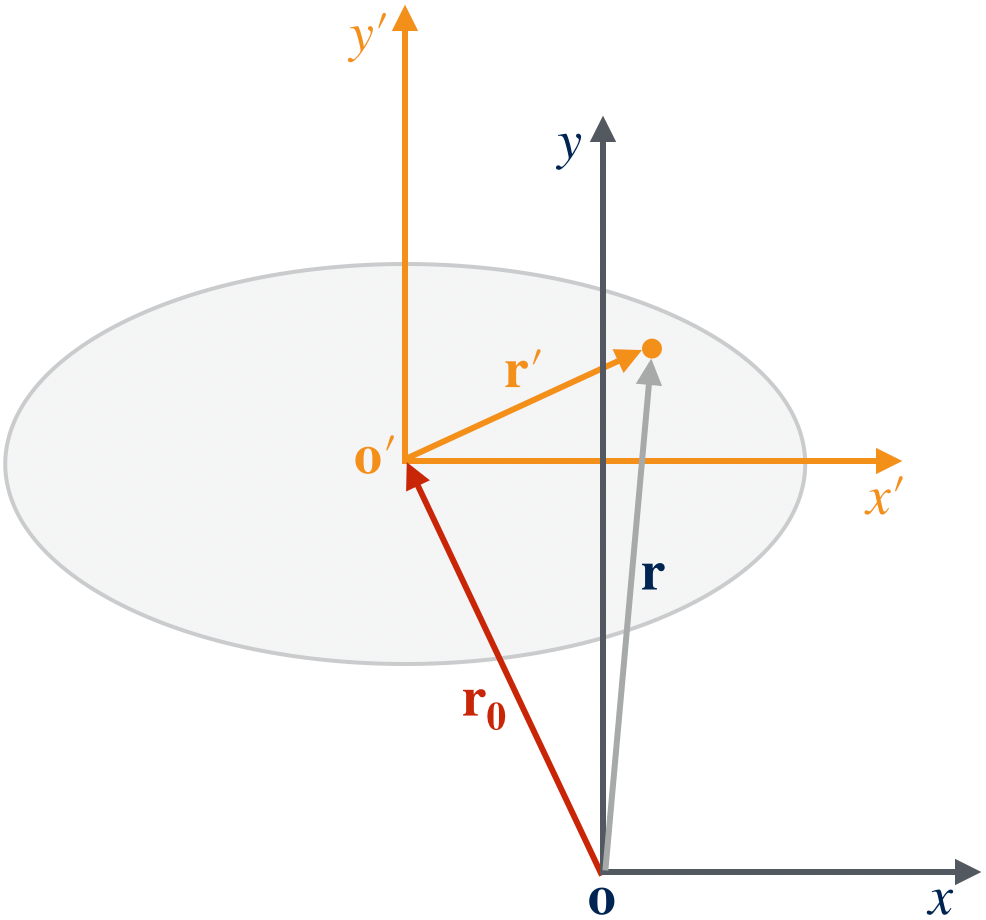
Now any point in the body (and the boundary) of the scatterer can be described by two position vectors: a vector in the reference coordinate $\vr$ and a vector in the internal coordinate $\vr’$. We can then transform the position vector $\vr$ to the internal coordinate using the translation operator:
\[\begin{equation} \vr' = T\vr = \vr - \vr_0 \end{equation}\label{eq:translation}\]or vice versa, we can transform the position vector in the internal coordinate $\vr’$ to the reference coordinate using an inverse translation operator:
\[\begin{equation} \vr = T^{-1}\vr' = \vr' + \vr_0 \end{equation}\label{eq:inverse_translation}\]The inverse translation operator is denoted as $T^{-1}$. It is clear now the translation operator subtracts the translation vector from the vector it applies to, while the inverse translation operator does the opposite: it adds the translation vector to the vector it applies to. The translation vector will always mean that it transforms a vector from the reference coordinate to the internal coordinate of a scatterer. With these assumptions, we can informally express the translation operator explicitly:
\[\begin{equation} T = \vr_0 \end{equation}\label{eq:explicit_translation_operator}\]and the inverse translation operator
\[\begin{equation} T^{-1} = -T = -\vr_0 \end{equation}\label{eq:inverse_translation_operator}\]Following this formalism, we can rewrite eq.\eqref{eq:translation} and eq.\eqref{eq:inverse_translation} as
\[\begin{equation} \begin{split} \vr' &= T\vr = \vr - T \\ \vr &= T^{-1}\vr' = \vr' - T^{-1} \end{split} \end{equation}\label{eq:translation_rewritten}\]It can be seen that in this formalism, we can treat translation and inverse translation consistently: applying a translation operator (either direct or inverse) to a vector results in a new vector which is the difference between the old vector and the operator itself.
Note that the translation vector here is denoted as $\vr_0 = o’ - o$ instead of $\vt$ because $\vr_0$ is commonly used to denote the position of an object in space, and it coincides with the translation vector in the present setup.
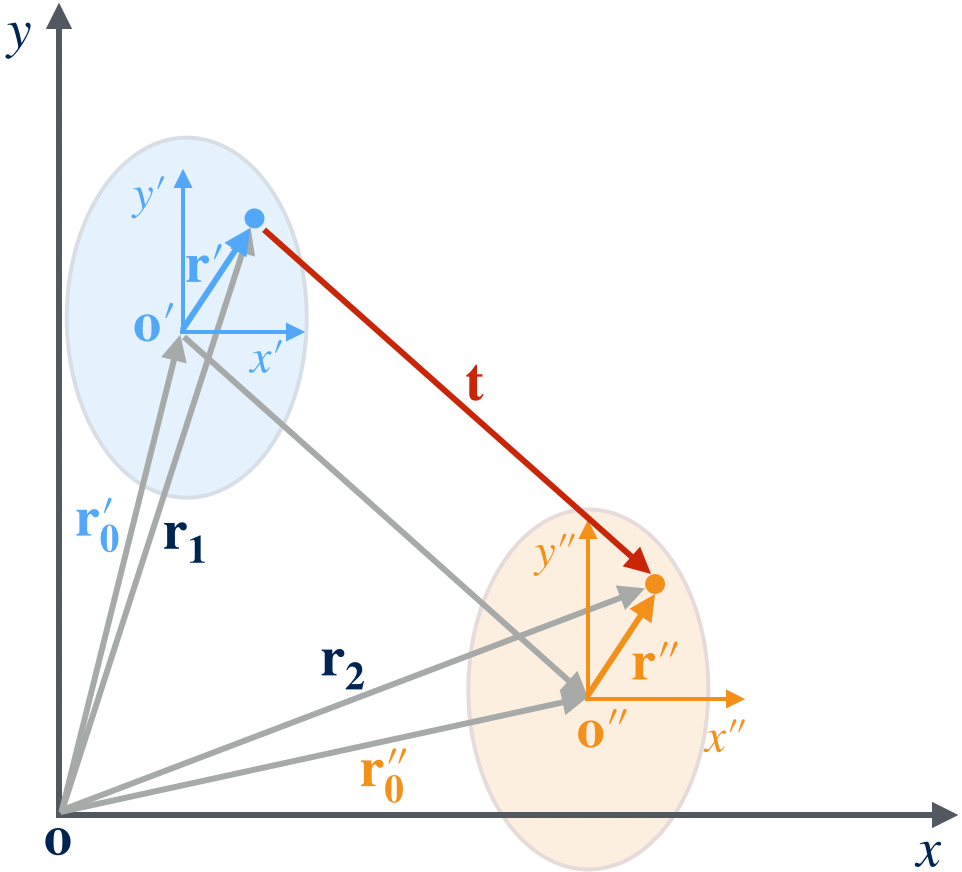
Sometimes, we will want to translate a scatterer from position $o’$ (described in the reference coordinate) to a new position $o’’$ (also described in the reference coordinate) as illustrated in Figure 4. Suppose we only know the translation operator of the old internal coordinate $T_1$ and the translation vector $\vt = o’’ - o’$ of between two internal coordinates. How can we express the new translation operator, $T_2$, for the translated scatterer locates at $o’’$ in terms of $T_1$ and $\vt$?
The translation operator for the old internal coordinate is
\[\begin{equation} T_1 = \vr_0' \end{equation}\]From Figure 4 we see that the new position vector of the origin of the translated scatterer is
\[\begin{equation} \vr_0'' = \vr_0' + \vt = T_1 + \vt \end{equation}\]Therefore the new translation operator is
\[\begin{equation} T_2 = \vr_0'' = T_1 + \vt \end{equation}\]Or more simply, if we know the position vector or the point of the origin of the translated scatterer in the reference coordinate, $\vr_0’’ = o’’ - o = o’’$, we can write $T_2 = \vr_0’’$.
Implementation
With a clear understanding of the translation of a scatterer, we will now start to implement it in a submodule translation.jl for Scattering.jl. First it is convenient to define an abstract type to describe any translation operators which shall be useful for later extension:
1
abstract type AbstractTranslation end
Then we will define a concrete type for a translation operator:
1
2
3
struct Translation{T <: Real} <: AbstractTranslation
t::Vector3D{T}
end
It only has one field which is a vector of three components. Vector3D is a constant defined as
1
2
using StaticArrays: SVector
const Vector3D{T} = SVector{3,T}
Here the sized array provided by the StaticArrays.jl package perfectly fits our use.
It is helpful to add a convenient constructor which accepts a Vector or three components separately
1
2
Translation(t::Vector{T}) where {T<:Real} = Vector3D(t) |> Translation
Translation(x::Real, y::Real, z::Real) = Translation([promote(x,y,z)...])
The promote method is provided by the Julia Base. It ensures the input x,y,z have same type which is required by the default constructor.
The chaining operator |> is extremely useful to increase the readability of the code. The output of the left operand of |> will be sent to the right operand as its input arguments. We can chain as many methods as possible together.
Conversion
A Translation instance is merely a three-component column vector. Thus it is sensible to convert any three-component column (or row) vector into a Translation instance. Julia provides a consistent way to deal with such situation. What we do is to provide additional convert method to the Julia Base:
1
2
import Base.convert
convert(::Type{T}, t::Vector3D) where {T<:AbstractTranslation} = Translation(t)
Note that it is necessary to import convert before addition. Otherwise, the new convert method will be invisible to users.
Math operations
As an operator, a Translation instance may support some math operations. The first one is applying it to a vector, which transform the vector into the coordinate system encoded in the Translation operator. Like matrix multiplication, we can use * to carry out the translation operation:
1
2
import Base.*
*(T::AbstractTranslation, v::Vector3D{S}) where {S<:Real} = v - T.t
It implements eq.\eqref{eq:translation_rewritten}.
There should be an unit operator for a translation operator such that it operates on a vector will return the vector itself. Thus the unit operator is actually a zero vector which we can implement it by extending Julia Base:
1
2
import Base.one
one(T::Translation{S}) where {S<:Real} = zero(T.t) |> Translation
Note that the translation operator has no zero operator. And as discussed earlier, the translation operator can be inversed as in eq.\eqref{eq:inverse_translation_operator}. It is also easy to implement:
1
2
import Base.inv
inv(T::S) where {S<:AbstractTranslation} = Translation(-T.t)
And we can also chain two translations together to produce a single equivalent translation since
\[\begin{equation} \begin{split} T_2T_1\vr &= T_2(\vr-T_1) \\ &= (\vr - T_1) - T_2 \\ &= \vr - (T_1 + T_2) \\ &= (T_1 + T_2)\vr \end{split} \end{equation}\label{eq:chain_translation}\]Therefore, we have
\[\begin{equation} T_2T_1 = T_1 + T_2 \end{equation}\label{eq:chain_translation2}\]This composition of translations shall be implemented as
1
*(T1::AbstractTranslation, T2::AbstractTranslation) = (T1.t + T2.t) |> Translation
Finally, it is convenient to extends Base.== to compare two translation operators whether they are identical:
1
==(T1::AbstractTranslation, T2::AbstractTranslation) = T1.t ≈ T2.t
The ≈ operator is an synonym for Base.isapprox method.
The implementation of the translation.jl module is done. And it is less than 20 lines of codes which is amazing!
Usage
Now we can perform translation operations using the Scattering.jl package in the Julia REPL as follows
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
julia> using Scattering
julia> using Test
julia> t = Vector3D(1.0, 2, 3);
julia> T1 = Translation(t) # create a translation operator from a vector
Translation{Float64}([1.0, 2.0, 3.0])
julia> inv(T1) # inversing an operator
Translation{Float64}([-1.0, -2.0, -3.0])
julia> v = Vector3D(1.0, 1, 1);
julia> @test one(T1) * v == v # unit operator do nothing
Test Passed
julia> T1 * v # transform v to T1's internal coordinate
[0.0, -1.0, -2.0]
julia> @test one(T1) * T1 == T1 # unit operator do nothing
Test Passed
julia> T2 = Translation(1.0, 1.0, 1.0) # create operator from three numbers
Translation{Float64}([1.0, 1.0, 1.0])
julia> T2 * T1 * v # apply composite operators on a vector
[-1.0, -2.0, -3.0]
Acknowledgements
This work is partially supported by the General Program of the National Natural Science Foundation of China (No. 21873021).