Brief introduction to the scattering theory and the Julia programming language
Julia in Practice: Building Scattering.jl from Scratch (1)
This is the first post of a series of blog posts published in Yi-Xin Liu’s research group website on an effort to demonstrate how to develop a software package for computing scattering and diffraction curves of individual or self-assembled nanoparticles, polymers as well as biological materials using Julia programming language. The purpose of this series of blog posts is in three folds: (1) to provide a source of concise understanding of the scattering theory especially for small angle X-ray scattering (SAXS); (2) to demonstrate the power of the Julia programming language in scientific computing; and (3) to serve as a detailed documentation for the Scattering.jl software package.
Table of Contents
Scattering Theory
Characterization tools based on the scattering theory are one of the most important techniques that provide the structural information of materials in various length scales from angstrom to micrometer. Typical scattering techniques are light scattering (LS), wide angle and small angle X-ray scattering (WAXS, SAXS), electron diffraction (ED), and neutron scattering (NS), depending on which type of the source of the incident beam has been utilized. Unlike imaging (real space) techniques, such as transmission electron microscope (TEM) and atomic force microscope (AFM), scattering techniques collect data in reciprocal space. Here “Reciprocal” means the information of large length scale (either feature size or distance) will be encoded in the small angle (low $q$) end of the scattering data. Thus the wavelength of different source beams determines its ability to detect objects in different length scales.
Imaging techniques typically will focus on a small region of a sample and only selected images are reported. Thus the data are always biased. As compared to imaging techniques, an important advantage of the reciprocal tools is that they gather the structural information in a sense of ensemble average (both time and space) of the entire volume of the sample. Other advantages include non-destructive measurements, ease to conduct in-situ measurements and measuring samples in their native states.
The aim of this series of posts is in two fold. Firstly, we want to develop a useful software package, Scattering.jl, that provides a consistent API to compute various scattering functions of arbitrary scatterers and their ordered or disorder assemblies in arbitrary length scales. Using this package as a starting point, we can perform more advanced analysis and simulations. For example, one can infer the size, shape, and arrangement of scatterers from the experimental scattering curves using various fitting models and algorithms. In particular, machine learning technique should be especially powerful in dealing with such inverse problems. Secondly, we want to take this opportunity to demonstrate the power of Julia programming language which is believed to be the language of choice for scientific computing.
To achieve this, a clear overview of the scattering theory is a must. As a topic having such a long history and spreading across almost every scientific field, huge amount of resources are scattered around and their notations are a mess. It is challenging to give a consistent formalism of the scattering theory. Fortunately, we have noticed several excellent papers with great readability on this topic.123 Here we give a briefly summary of their work. It should lay a solid foundation for our following development work. Details and derivations are deferred to later posts.
The general expression for scattering intensities is simply an ensemble average intensities contributed by every elementary scatterers (e.g. electrons):
\[\begin{equation} I(\vq) = \ensemble{\abs{\sum_{n=1}^N \rho_n\exp{\left(i\vq\cdot\vr_n\right)}}^2}. \end{equation}\label{eq:I-general}\]The total number of elementary scatterers is $N$. $\rho_n$ is the scattering contribution of scatterer $n$, $\vr_n$ is the position vector of scatterer $n$ and $\vq$ is the scattering vector [$q=\abs{\vq}=(4\pi/\lambda)\sin\theta$, where $\theta$ is half the scattering angle and $\lambda$ is the wavelength of the incident beam].
The summation in the above equation can be split into multiple summation by decomposing the position vector into a sum of several relative vectors, each of which shall represent a conceptual or realistic objects. For example (see the following figure), a periodic lattice of particles can be first divided into unit cells. Each unit cell consists of several motifs. Lastly each motifs may consist of a bunch of elementary scatterers.
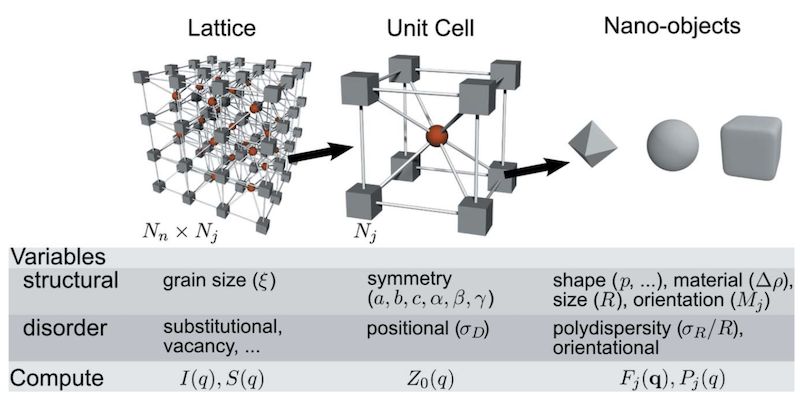
For periodic lattices, after some derivations, and further considering the distribution of sizes and orientations and variation of scatterer positions due to thermal fluctuations, the final expression for the scattering intensities is
\[\begin{equation} I(q) = P(q)\left[ \frac{cZ_0(q)}{P(q)}G(q) + 1 - \beta(q)G(q) \right] \end{equation}\label{eq:I-periodic}\]Clearly, we have four quantities in total to compute: $P(q)$, $Z_0(q)$, $\beta(q)$, and $G(q)$.
$P(q)$ is the form factor of the periodic lattice, which is simply a sum over the form factor of all motifs in the unit cell when the interparticle correlation is ignored.
\[\begin{equation} P(q) = \sum_{j}P_j(q) = \sum_j \ensemble{\abs{F_j(\vq)}^2}_{od} \end{equation}\label{eq:Pq}\]where $F_j(\vq)$ is the form factor of motif $j$, the subscripts $o$ and $d$ stand for average over orientation and size distribution, respectively. Hence, it is essential we can develop a code to compute the form factor of each motif. Typical motifs are spheres, cylinders, core-shell particles, and polygons in nanoparticle system. For simple shapes, there may be an analytical expression for the form factor. For arbitrary shapes, however, we shall compute it numerically. The computation of $F(\vq)$ should be the core of our software package.
$Z_0(q)$ is the lattice for the periodic lattice, which can be computed as
\[\begin{equation} Z_0(q) = \frac{1}{q^2} \sum_{\lbrace hkl \rbrace} \abs{\sum_j\ensemble{F_j(\mM_j\cdot\vq_{hkl})}_d\exp[2\pi i(x_jh + y_jk + z_jl)]}^2 L(q - q_{hkl}) \end{equation}\label{eq:Z0}\]The equation above seems scary. But don’t panic, we will dive into every details about it in later posts. At present, only you should know is that the form factor of a motif is still the most important object.
The function $L(x)$ is a function which mimics the shape of scattering peaks. Since this function is less involved in the whole theory, it serves as a good starting point of the development of our package. The best way to learn is PRACTICE, PRACTICE, PRACTICE! (Important things shall echo three times.) Thus the next post of this series will be dedicated to developing a submodule of the Scattering.jl that computes $L(x)$.
Other quantities, $\beta(q)$ and $G(q)$, account for the effect of size distribution of scatterers and encodes fluctuations of the scatterer positions, respectively. They will be our topics after the computation of $F(\vq)$, $P(q)$ and $Z_0(q)$ is implemented.
Why Julia
I ran into Julia about five years ago. Back to those days, I was in love with Python which greatly increased my coding productivity. However, I was suffering from its slowness. Before Python, I developed scientific software using C++ which is fast but it is too complicated and sometimes it made me crazy to implement a specific numerical algorithm. You can check out those software packages I have developed here. I was wondering then if there was a programming language which combines the performance of C++ and productivity of Python. I tried to search terms like “speed and scripting programming language” in Google and I found Julia, which was in its very early stage but showed its great potential. After that, I payed special attention on it. Now Julia is in version 1.3. After ten years intensive developing, it matures into a stable language. Therefore I decide to give it a try. Scattering.jl is my first package written in Julia.
Besides its speed (check out a comparison of performance of various popular programming languages here), what attracts me most are listed below:
- The syntax is even more clean and concise than Python.
- Julia’s mathematical syntax makes it an ideal way to express algorithms just as they are written in papers, owing to the support of Unicode characters and other syntax sugar added by the language. This drastically increase the readability and maintainability of the code.
- Multiple dispatch mechanism (allowing multiple functions to have the same name) allows you to write reusable codes more easily. And the functionality is smooth to be extended by others.
- High level support for GPU computing and parallel programming.
- Production ready numerical and machine learning packages: the state-of-the-art differential equations ecosystem (DifferentialEquations.jl), optimization tools (JuMP.jl and Optim.jl), iterative linear solvers (IterativeSolvers.jl), a robust framework for Fourier transforms (AbstractFFTs.jl), and powerful tools for deep learning with automatic differentiation and GPU acceleration (Flux.jl).
Nature published an article to promote Julia: Julia: come for the syntax, stay for the speed.
Let’s get a little bit of taste of Julia:
1
2
P(x, μ, σ) = 1/(√(2π)*σ) * exp(-(x-μ)^2/(2σ^2)) # Gaussian distribution
C(r) = 2π*r # compute circumference of a circle
And the Python equivalence:
1
2
3
4
5
import numpy as np
def P(x, mu, sigma)
return 1/(np.sqrt(2*np.pi)*sigma) * np.exp(-(x-mu)**2/(2*sigma**2))
def C(r)
return 2*np.pi*r
Now it is time to get our hands dirty! See you in the next post.
Acknowledgements
This work is partially supported by the General Program of the National Natural Science Foundation of China (No. 21873021).
References
-
Li, T.; Senesi, A. J.; Lee, B. Small Angle X-Ray Scattering for Nanoparticle Research. Chem. Rev. 2016, 116, 11128–11180. ↩
-
Senesi, A. J.; Lee, B. Small-Angle Scattering of Particle Assemblies. J. Appl. Crystallogr. 2015, 48, 1172–1182. ↩
-
Yager, K. G.; Zhang, Y.; Lu, F.; Gang, O. Periodic Lattices of Arbitrary Nano-Objects: Modeling and Applications for Self-Assembled Systems. J. Appl. Crystallogr. 2013, 47, 118–129. ↩