Research Projects
Research interests of our group focus on developing theoretical and numerical methods for understanding the phase behavior and structures of block copolymers, polymer brushes and polyelectrolytes both in bulk and under geometrical confinements.
We also conducted both experimental and theoretical studies to elucidate the fundamental mechanism of polymer crystallization, using monolayer crystals of low molecular weight poly(ethylene oxide) (PEO) fractions as a model system.
Table of Contents
1. Self-Assembly of Block Copolymers Under Soft Confinements
Block copolymers represent an important class of polymeric materials that can self-assemble into complex microstructures on the scale of 1 to 100 nm. Confining block copolymers in geometrical environments introduces additional parameters, which leads to an even richer set of nanostructures, making it an attractive route for a wide range of applications including nanolithography, nanotemplating, nanoporous membranes, coatings, and biomaterials. Our group have conducted a comprehensive study of the confining system of block copolymers, including development of highly efficient numerical tools, the surface states of polymer brushes which are often used to modify substrate properties, development of a model to describe the interaction between the modified substrates and the block copolymers, thermodynamic and kinetic aspects of directed self-assembly (DSA).
1.1 Methodology Development
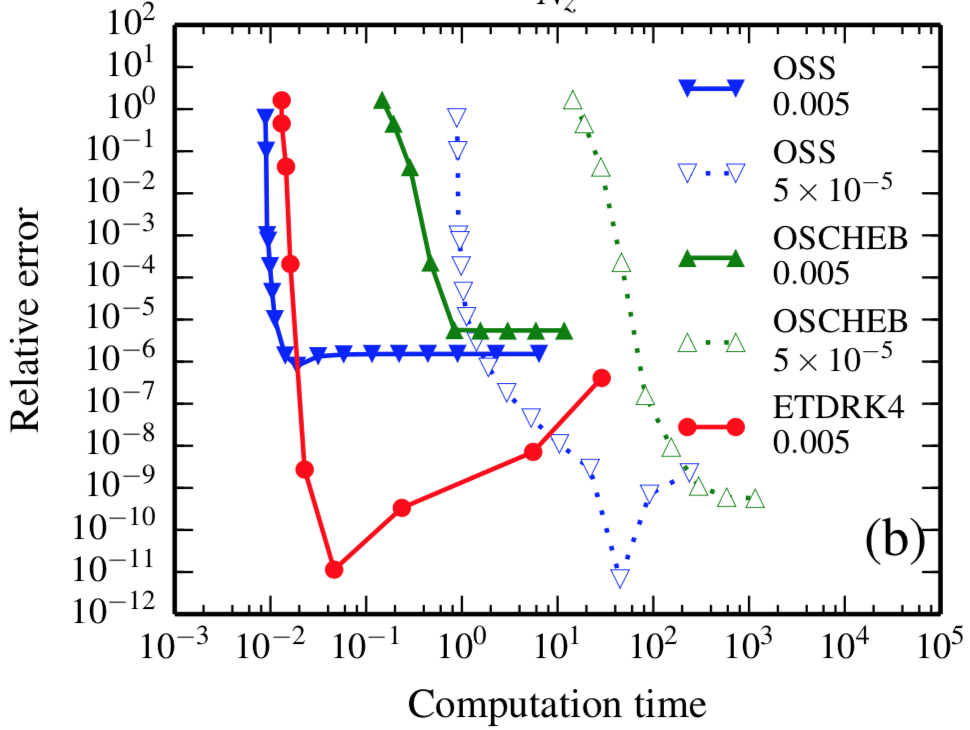
The most popular approach for solving the set of self-consistent field theory (SCFT) equations for bulk systems, the operator splitting algorithm based on pseudo-spectral method, suffers from poor convergence rate and low accuracy when applying to confining systems. The main issue is that the non-periodic boundary conditions due to the constraints of the substrates impose serious difficulties during solution of the modified diffusion equations (MDEs) of SCFT. We developed an exponential time differencing method, ETDRK4, based on Chebyshev collocation, which is specially designed to handle non-periodic boundary conditions more efficiently. It is demonstrated that this method exhibits fourth order accuracy in contour stepping and meanwhile retains the ideal exponential convergence rate in spatial dimensions. (J. Chem. Phys., 2014, 140, 224101.)
1.2 Polymer Brushes
- Chinese J. Polym. Sci., 2018, 36, 1047-1054.
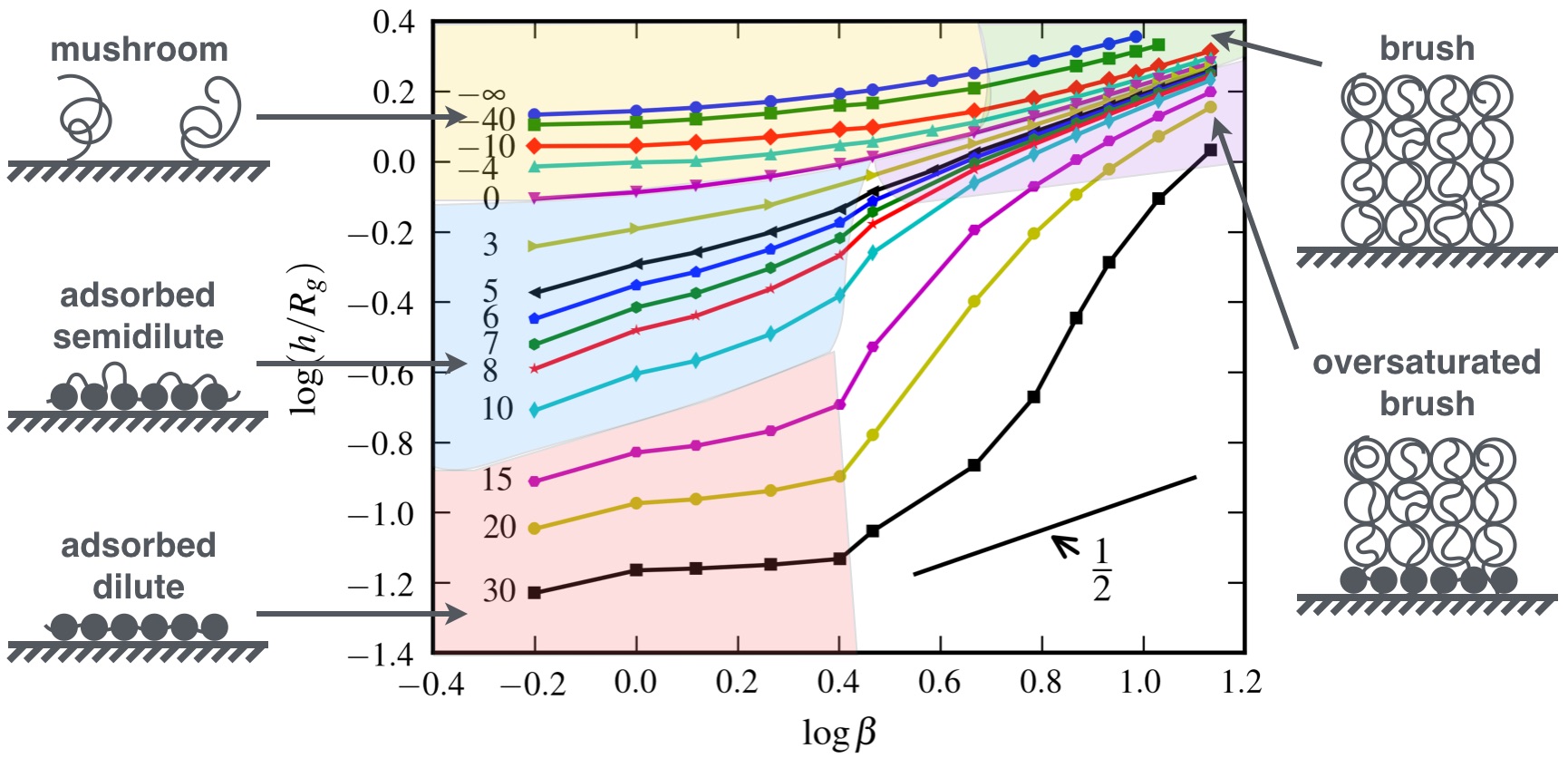
Polymer Brushes, being polymer chains with one end tethered to solid surfaces or interfaces by covalent bonds, have been often used to modify the surface properties of substrates, which further control the self-assembled structures of block copolymers confined by these substrates. Previous theoretical and numerical studies mainly focused on the behavior of polymer brushes on neutral or purely repulsive surfaces. However, both neutral and purely repulsive substrates are rare in practice. Owing to our newly developed numerical method, ETDRK4, we can treat polymer brushes on interacting surfaces being either attractive or repulsive to the grafting polymers. It is found that the brush state of the grafting polymers exists at high surface coverage for a whole range of surface interactions from complete repulsion to strong attraction. Three additional surfaces states were identified by a scaling analysis of the layer thickness as a function of the stretching parameter at different surface interactions.
1.3 Surface Interaction Model
- J. Chem. Phys., 2016, 145, 214902.
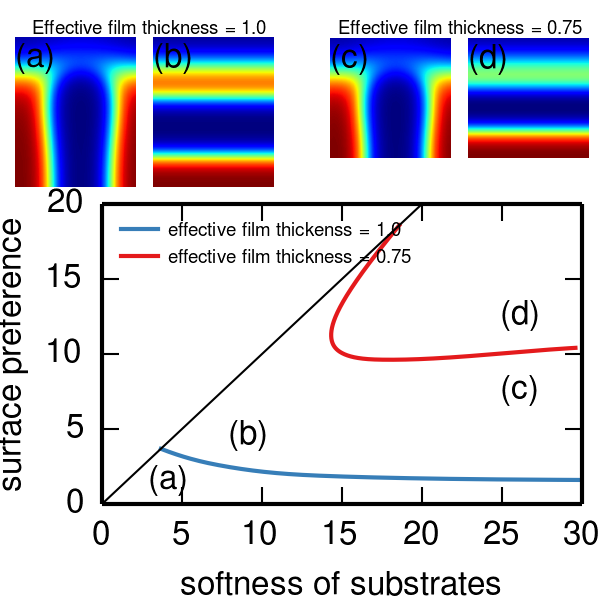
The surface interaction between substrates and block copolymers is one of the most important factors that control the alignment of self-assembled domains under thin film confinement. Most previous studies simply modeled substrates modified by grafting polymers as a hard wall with a specified surface energy, leading to an incomplete understanding of the role of grafted polymers. We proposed a general model of surface interactions where the role of grafted polymers is decomposed into two independent contributions: the surface softness ($\gamma$) and the surface preference ($\delta$). With this separation, we elucidate the connection among bare hard wall confinement (SST), hard confinement modeled by the “masking” technique, and soft confinement. Soft confinement reduces to the mask hard confinement at large $\gamma$ and to the SST hard confinement in the limit of $\gamma\to\infty$. It is also possible to map the soft confinement model using ideal random copolymer-grafted substrates onto our model. Hence we believe that this separation of surface interactions into two independent parts are universal as long as no internal phase separation occurs across the confining wall itself.
Based on this model of surface interactions, we show that the homopolymer-grafted confinement is indeed a versatile platform for creating stable perpendicular lamellae that should be seriously considered in experiments and industrial applications. By varying the surface softness and the surface preference of the confining wall, we identify a reasonable window of perpendicular lamellae in the phase diagram of the alignment of self-assembled domains even when the confining wall is highly selective to one of blocks of the block copolymer. It thus brings more options in devising substrates that favor perpendicular lamellae by tweaking other properties of substrates that are hopefully easier to control such as the composition, length, and/or grafting density of grafted homopolymers.
1.4 Directed Self-Assembly (DSA)
Directed self-assembly (DSA), which utilizes chemoepitaxy or graphoepitaxy to guide the microphase separation of block copolymers (BCPs), is a competitive next-generation lithography candidate for electronic industry. Based on this technique, large scale defect-free ordered nanostructures, have been successfully produced on patterned substrates in experiments. In general, sparsely patterned templates are preferred because the template is produced by photolithography whose cost is proportional to the resolution of the template. However, the directing ability of the template weakens as the pattern in the template becomes sparser. Consequently, it is impossible to reduce the cost by lowering the resolution of the template without limitation.
1.5 Machine Learning Assisted Inverse Design of DSA Templates
- ACS Appl. Mater. Interfaces, 2023, 15, 31049-31056.
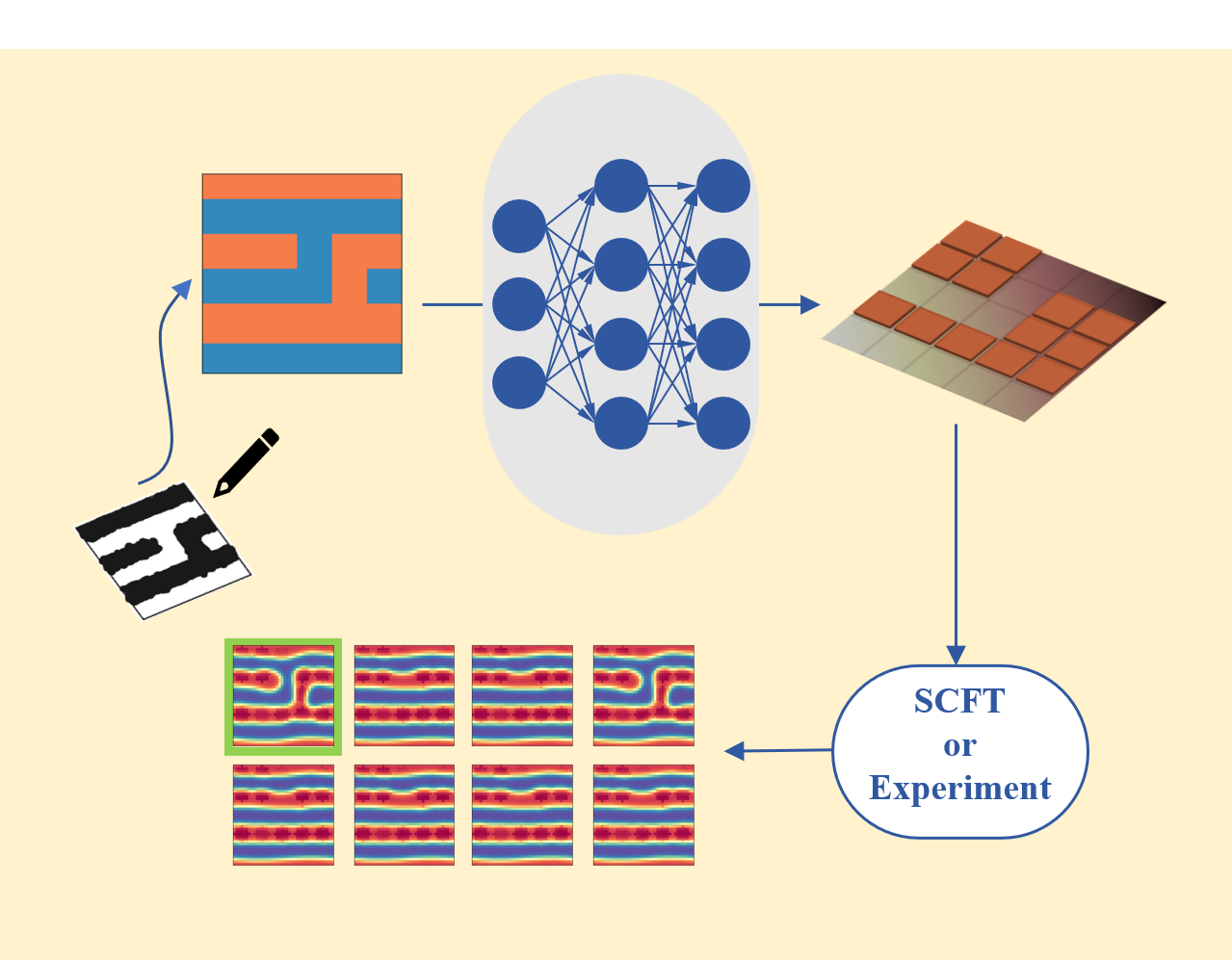
Inverse design is an emerging concept in materials design that the desired functionality of the new material is declared first and theoretical or numerical calculations are then used to predict which stable compounds/molecules exhibit the required functionality. The common approach for tackling such inverse problems is converting them into optimization problems and optimization methods (such as evolutionary algorithms) are employed to solve these problems. One major issue of this approach is that the optimization method has to be rerun once the desired functionality is changed a little. To settle this issue, we propose a machine learning approach based on deep learning and neural networks for inverse design. One of the advantages of the machine learning approach is that once the model is trained, we can use it again and again. Note that the predicting stage of the machine learning is blazing fast. Thus it can save tremendous amount of computational time in practical applications.
1.6 Removal of Defects in Self-Assembled Thin Films
- Acta Polym. Sin., 2018, 12, 1548-1557.
- Macromolecules, 2018, 51, 4201-4212.
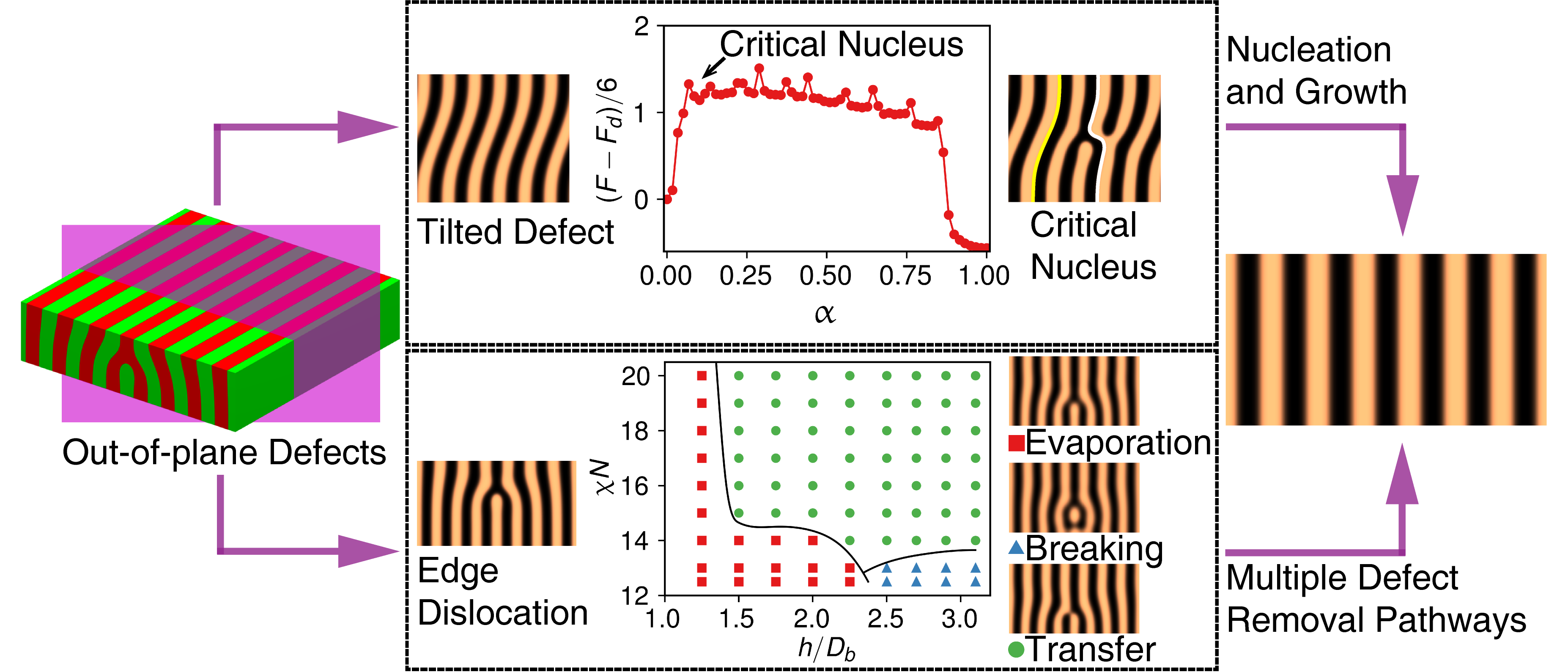
Understanding the defect removal process is crucial for fabricating defect-free self-assembled structures in block copolymer thin films. Grafting polymers onto substrates is a widely accepted way to control domain orientations and to fabricate surface patterns for DSA. However, the role of the grafted polymers on defect removal remains unclear. We employed the string method coupled with SCFT to explore the influence of grafted polymers on the removal of a dislocation dipole in lamellar-forming thin films assembled by AB symmetrical diblock copolymers. It is found that the “immersion effect” and the “rearrangement effect” of the brush layer can facilitate the hopping diffusion of block copolymer chains through reducing the effective Flory-Huggins interaction parameter, thus making the formation of the “bridge” structure more easier. The increase of the softness (decreasing $\gamma$) of the brush layer will enhance these two effects and reduce the energy barrier of the transition state of the defect removal process. In the limit of extremely soft confinement, the bridge structures already exist in the dislocation dipole near the brush layer, leading to a diminishing energy barrier of the removal process.
Most previous studies mainly focused on the removal of in-plane dislocation and disclination defects, while out-of-plane defects receive less attention. We studied in detail the removal of two types of out-of-plane defects of lamellar forming block copolymer thin films, the tilted domain defect and the cross-sectional edge dislocation defect, using the string method coupled with the numerical SCFT. It is found that the removal of the tilted domain defect can be regarded as an order-order transition process (OOT) controlled by the nucleation and growth mechanism. On the other hand, the cross-sectional edge dislocation can be eliminated by either evaporating or growing its core (a partial domain). For both cases, multiple removal pathways have been identified by varying the height of the partial domains and the segregation strength of the block copolymer. Phase-diagram-like maps are constructed to show which removal pathway can occur most probably at given height and segregation strength. In strong segregation regime, in consistent with that found in the removal of in-plane defects, one or more bridge structures are formed, which serve as a channel for diffusion of polymer chains. When the segregation is weak, however, no actual bridge but only a nascent bridge structure, whose density of A components in the B domain is slightly higher than the averaging value, is observed and plays a similar role as the actual bridge.
1.7 Research Notes
- A Quick Guide to the Self-Consistent Field Theory in Polymer Physics
- Lecture Notes in Polymer Physics
2. Self-Assembly of Block Copolymers in Bulk

2.1 Methodology Development
- Chinese J. Polym. Sci., 2018, 36, 488-496.
SCFT, as the state-of-the-art technique for computing the self-assembled structures of block copolymers, is attracting continuous efforts to improve its accuracy and efficiency. Inspired by the ETDRK4 method we developed to solve non-periodic problems (confined systems), we have extend it to the periodic problems, i.e. bulk systems. By making a careful comparison with currently most efficient and popular algorithms, we have shown that the periodic-ETDRK4 method significantly reduces the number of chain contour steps in solving MDEs, resulting in boost of the overall computational efficiency. It is the most efficient non-parallel algorithm for bulk SCFT calculations to date.
2.2 Block Copolyelectrolyte Solutions
- Macromolecules, 2011, 44, 8261-8269.
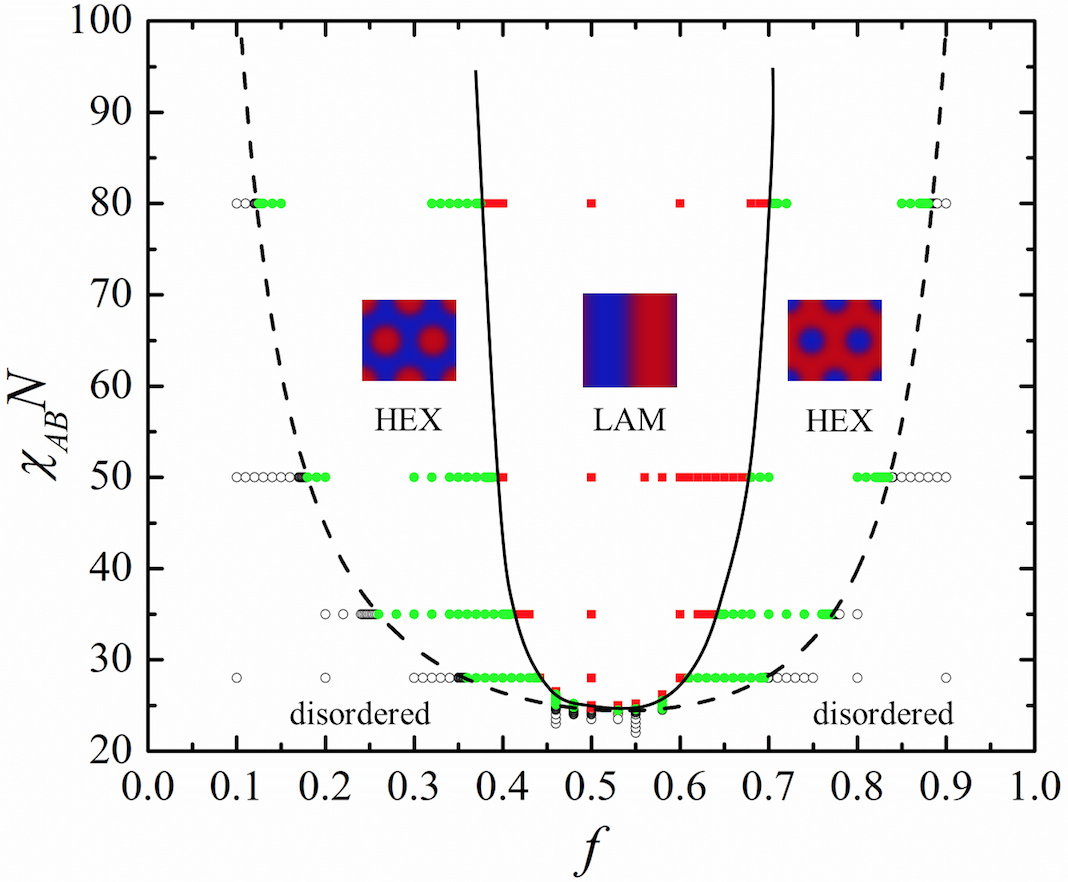
We studied the microphase separation of charged diblock copolymers by SCFT. While earlier SCFT studies on charged systems are mostly restricted in one-dimensional (1D) space, we successfully extend the SCFT technique to two-dimensional (2D) space or higher by introducing the {\bf multigrid method} to solve the Poisson-Boltzman equation arising from electrostatic interactions. The phase diagram of the charged-neutral (A-B) diblock copolymer solution in $\chi_{AB} N \sim f$ space was then constructed by SCFT calculations. It is found that The order-disorder transition (ODT) line and the order-order transition (OOT) line were both higher than those in the neutral diblock copolymer solution. Meanwhile, the ODT line and the OOT line are asymmetric. These features of the phase diagram lead to larger parameter space for the hexagonal phase (HEX) near $f=0.5$, which we believe explains the recent experimental results.
2.3 Fluctuation Stabilized Mesophase
- Macromolecules, 2017, 50, 6263-6272.
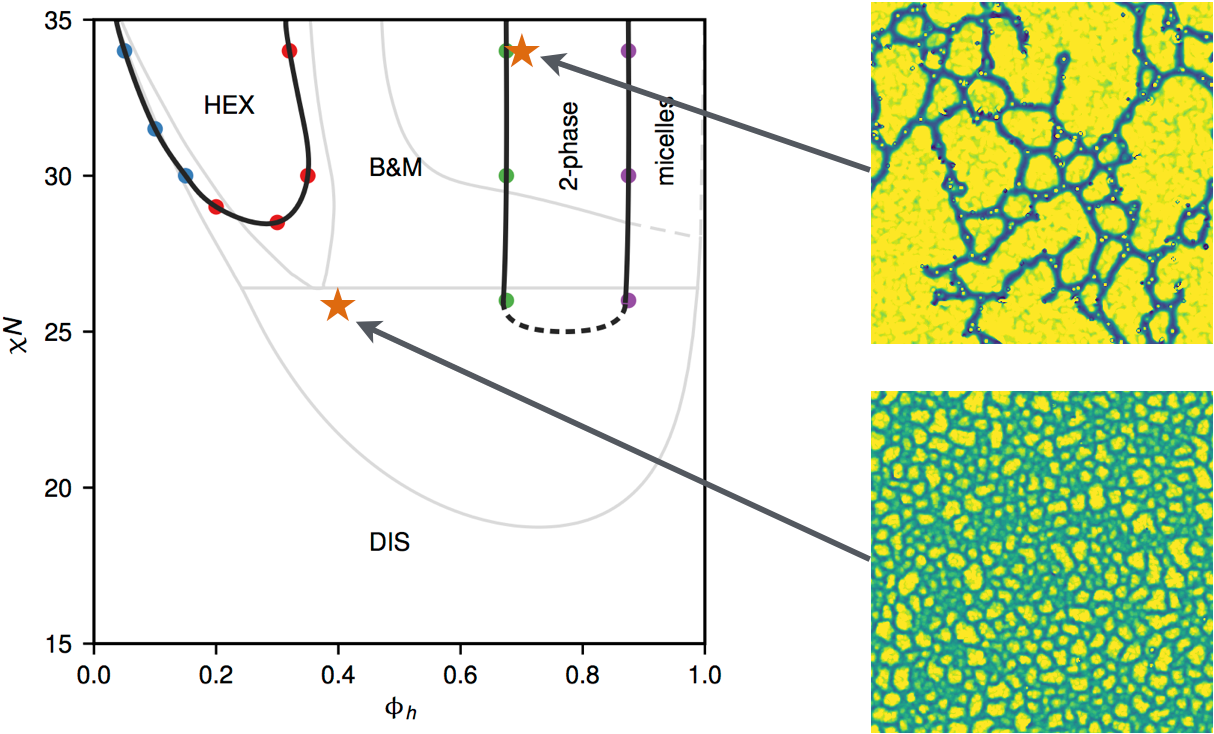
A new class of thermoplastic elastomers possessing unusual mechanical properties has recently been discovered in binary blends of A-b-(B-b-A’)$_n$ miktoarm star block copolymers and A homopolymers that spontaneously form an unusual, thermodynamically stable, aperiodic “bricks-and-mortar” (B&M) mesophase morphology. The B&M mesophase is believed to be stabilized by thermal fluctuations, as in the well-known case of the bicontinuous microemulsion phase. In collaboration with Prof. G. H. Fredrickson at UCSB, we investigated the equilibrium self assembly of such miktoarm polymer binary blends using two-dimensional field-theoretic simulations. As expected, the B&M mesophase is not present in the mean-field phase diagram obtained with self-consistent field theory, but complex Langevin (CL) simulations, which fully incorporate thermal fluctuation effects, reveal dramatic changes to the phase diagram. A region of strong fluctuations results in the emergent stabilization of the B&M mesophase in a broad composition channel positioned between microphase separation and macrophase separation envelopes, consistent with experimental observations. Our simulations clarify the topology of the blend phase diagram and suggest that the B&M mesophase, at least as observed near the order-disorder transition, has no long-range or quasi-long-range positional or orientational order.
2.4 Beyond Mean-Field Density Functional Models for Polymer Systems
While SCFT achieves remarkable success in modeling self-assembly of block copolymers, it is a mean-field theory which ignores the fluctuating effects. Using beyond mean-field field-theoretic simulations to study fully fluctuating polymer systems remains a big challenge. Current field-based approaches are highly computational demanding which renders it infeasible to tackle large-scale problems. In collaboration with Prof. G. H. Fredrickson at UCSB, we propose a density functional model that can incorporate thermal fluctuations to describe polymer solutions. Meanwhile, it can cut the number of dimensions of the computational space from 4 to 3, leading to a reduction of computational cost for about two magnitude. Using the same strategy for developing the model of polymer solutions, it can be generalized to other polymeric systems such as block copolymers.
3. Ultrathin Film Polymer Crystallization
- Coord. Chem. Rev., 2010, 254, 1011-1037.
Ordering and crystallization of polymeric chains with regular chemistry structure is one of the most striking phenomena in condensed matter physics. The process of polymer crystallization is a transition from a randomly coiled state to a perfectly ordered state. During this process a hierarchy of ordered structure develops, which in turn controls the physical properties of the polymer materials. In bulk, spherulites are the most common superstruc-tures observed when crystallizing from melt, while single crystals and dendrites can be grown from dilute solutions. Recently, polymer crystallization under spatial confinement, especially in thin (thickness less than 1000 nm) and ultrathin (thickness less than 100 nm) films on solid substrates, has attracted increasing attention. The objective to study polymer crystallization confined in ultrathin films is twofold:
- to develop new technologies and to enhance device performance;
- to provide new evidence to better understand the nature of polymer crystal-lization.
Low molecular weight poly(ethylene oxide) (PEO) fractions tend to form integral folded chain [IF($n$)] monolayer crystals with $n$ the number of folds per chain on mica surfaces, which serve as a good model to study the underlying mechanism of polymer crystallization.
3.1 Crystallization Kinetics
- Macromolecules, 2011, 44, 8819-8828.
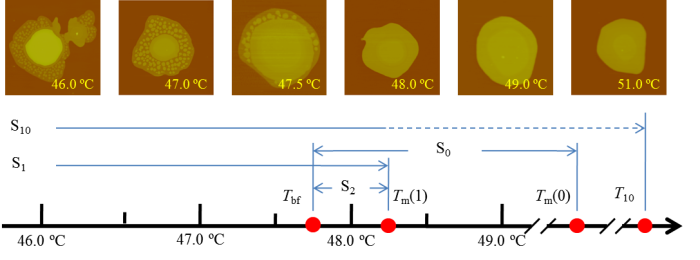
The phase selection pathways in crystallization of PEO monolayer on mica surfaces was intensively investigated by in situ atomic force microscopy (AFM). We focused on a temperature region where the crystallization kinetics of IF(0) and IF(1) crystals are expected to compete with each other. Four pathways are identified: melt$\rightarrow$IF(0) crystals (S0), melt$\rightarrow$IF(1) crystals (S1), IF(1) crystals$\rightarrow$IF(0) crystals (S10), and the composite fluctuation of the latter two (S2). This observation agrees with classical nucleation theory except the fact that S0 cannot occur before S1 when the undercooling exceeds some critical value, which can only be understood by introducing the Gr'an'asy-Oxtoby nucleation theory.
3.2 Crystal Thickening Process
- Macromolecules, 2009, 42, 2886-2890.
- Acta Polym. Sin., 2018, 9, 1212-1220.
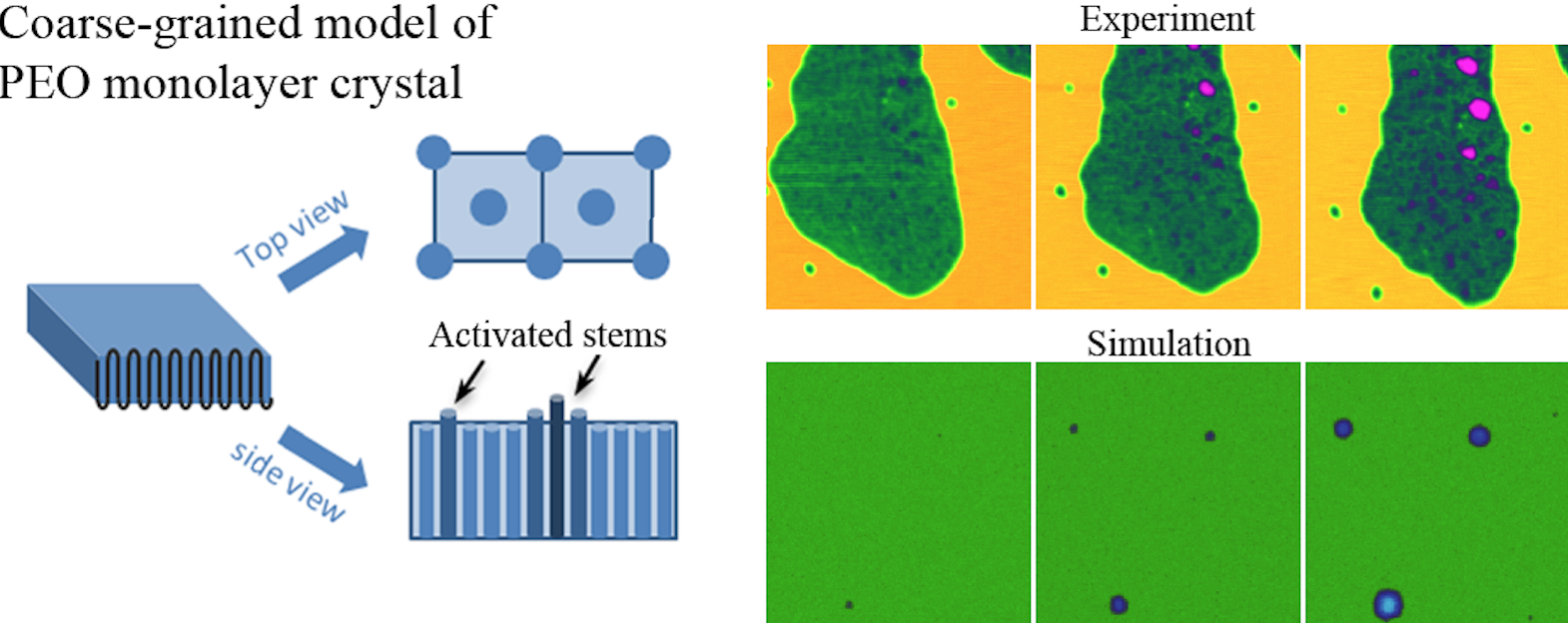
The thickening behavior of IF(1) monolayer crystals subjected to different annealing temperatures was also in situ followed by AFM and the morphological evolution was recorded sequentially. IF(0) crystals form via creating thickening domains within the IF(1) mother phase with an induction period. While the number of thickening domains increases with time, the thickness behaves a sigmoidal increase and lateral size increases linearly. This phenomenon highly indicates that lamellar thickening follows a nucleation and growth mechanism, which has been actually reproduced by phase field simulations. Combining the experimental and simulation results, we can conclude that while the longitudinal sliding diffusion within the crystalline lattice provides the manner of thickening, the fold surface free energy dominates the thickening barrier. As the fold surface free energy reduces with temperature (an effect has been neglected in most literatures), the thickening rate will increase.
3.3 Thermodynamic Behavior
Based on statistical thermodynamic analysis, we predict that the thickness of amorphous layers of IF(0) crystals increases with temperature, which is confirmed by crystallinity measurements and small angle X-ray scattering (SAXS) experiments.
The melting behavior of PEO monolayer crystals on mica surfaces was studied by AFM. Taking account of the linear decrease of fold surface free energy with temperature, we have shown that the relations between melting points and thickness and/or fold number can be described by a modified Gibbs-Thomson equation. The end group effect on the melting behavior of the monolayer crystals was also analyzed.
4. Scientific Software Development
As an important part of our research work, we have developed several scientific computing software and packages and implemented numerical algorithms to perform computational tasks for our research.
Currently, we almost exclusively use the Julia language. Previous software and packages developed in C/C++, Matlab, and Python are considered deprecated.
4.1 Software & Packages
Please visit the full list of our software. Below is a brief list of our core software:
4.2 Numerical Algorithms
- OPS method for constructing the phase diagram of polymer blends.
- Modern acceleration methods for SCFT calculations of block copolymers.
- Graph enhanced SCFT method for computing arbitrary noncyclic chain architecures.
- ETDRK4 and periodic-ETDRK4 methods for SCFT calculations of confined polymers.
- Chebyshev collocation method for SCFT calculations of confined polymers.
- Pseudo-spectral method for SCFT calculations.
- Multigrid method for SCFT calculations of charged polymers.
- Off-lattice Monte-Carlo simulation of polymer crystal growth.
- Phase-field simulations of thin film polymer crystal growth.
4.3 Research Notes
Please visist the full list of our Research Notes